つーさのくーかん

ここのところ毎日何かに打ちのめされて帰ってきている気がするω
もうなんか、自分が出来なすぎて、勉強するのがイヤになってしまいます。
というか、勉強がイヤだという人の気持ちが何となくわかった気がします。

本日も何か疲れたので自習さぼって早々に帰宅。

x^a = a^x の解答まがいなものを置いておきます。

x^a = a^x ⇔ log(x)/x = log(a)/a (a>0, x>0) 参照

f(x) = log(x)/x とおき、
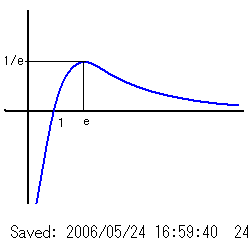
f(x)と y = log(a)/a との共有点の個数をaの値で分類する。

log(x)/x のグラフの概形を描くと、

(増減表略 グラフより読み取ってください)
lim(x->+0)f(x)=-∞
lim(x->∞)f(x)=0

で

(↑ペイントで書いた。歪んでるとか許せ。)

のようになる。

ここで、 y = log(a)/a の a は定数なので、
切片log(a)/aの水平な直線となり、このときの切片は、
f(a)で表すことができる。

よって

方程式の解の個数は

　0 ＜ a ≦ 1 のとき 1つ
　1 ＜ a ＜ e のとき 2つ
　　a ＝ e のとき 1つ
　　a ＞ e のとき 2つ